It’s midnight. You’re driving home after an evening out, when you notice a small bright object—or perhaps two—moving across your field of view in an odd scalloped pattern. Because you have seen one before, you may recognize it as the reflector on the wheel of a bicycle approaching on an intersecting street. You must quickly decide whether to stop, slow down, speed up, or continue at the same speed. To make that decision correctly, you must know not only how fast you are moving, but also when the bicycle will enter and leave the intersection. This is considerably more difficult than you may think.
Reflecting an Illusion
If the bicycle frame is dark and the rider is wearing dark clothing, the bicycle may be visible only because light from your car strikes a reflector on a wheel. You must judge the bicycle’s position, speed, and direction from the motion of the reflector, yet the reflector is not traveling in a straight line.
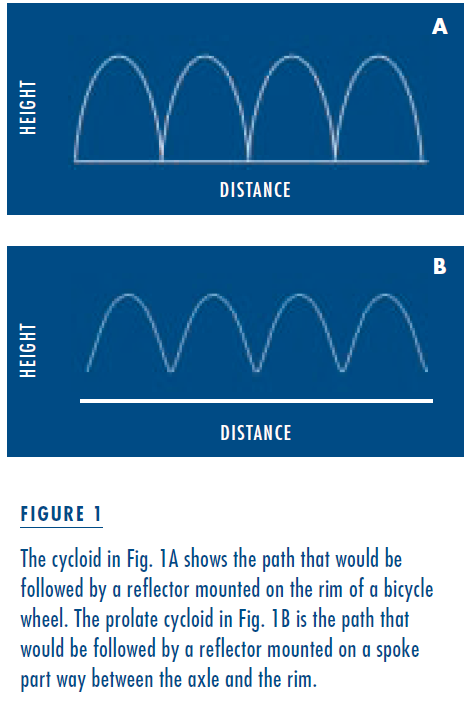The Code of Federal Regulations (Ch. II, Section 1512.16, 1-1-00 Edition) specifies that street bicycles have a reflector on each wheel, and that “the center of spoke-mounted reflectors shall be within 76 mm (3.0 in) of the inside of the rim. Side reflective devices shall be visible on each side of the wheel.” (The law allows for reflective sidewalls or rims instead, but these are not common.) Since the reflector must be near the inside of the rim rather than on the axle, its motion will be a combination of the linear forward (or translational) motion of the bicycle and the rotation of the wheel. The curve produced by combining a translation and a rotation is called a cycloid. Figure 1A illustrates a cycloid, showing the path that would be followed by a reflector if it were mounted directly on the rim of a bicycle wheel. However, a reflector can’t actually be mounted on the rim without interfering with the brakes, so it’s placed on a spoke inside the perimeter of the wheel. There its trajectory takes the shape of a prolate cycloid, as shown in Figure 1B.
There are several interesting things about the cycloid path. First, it is significantly longer than the path followed by the bicycle itself. Since the reflector must traverse its longer path in the same time that the bike travels a shorter distance, the average speed of the reflector must be greater than the speed of the bicycle itself. How much greater it is depends on the distance between the reflector and the axle.
Second, notice that the forward-moving (or translational) speed of the reflector is not constant. It progresses alternately rapidly and slowly. When the reflector is moving across the top of the wheel, its forward motion is rapid. When it is nearer the bottom of the wheel, it moves primarily up and down, exhibiting relatively little forward motion.
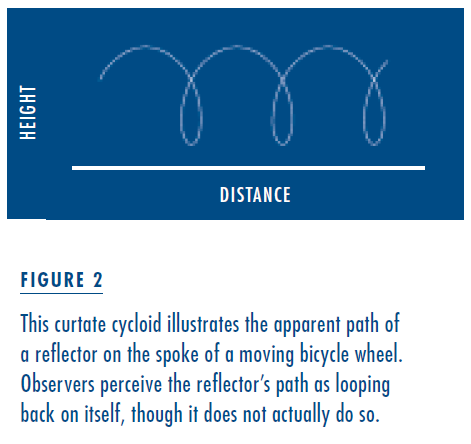Finally, note that the reflector never moves backwards. Its forward motion is not at a constant speed, but it never loops back on itself. If you have ever watched the reflector on a moving bicycle wheel, you may find this surprising. Most observers describe the apparent trajectory of the reflector as looking like the curtate cycloid drawn in Figure 2. But the only way the reflector could actually loop back on its path would be if the distance from the axle to the reflector were greater than the distance from the axle to the rim, which is, of course, not possible. So not only does the reflector traverse a longer path than the bicycle, but in our perception it travels even farther. Psychologist Dennis Proffitt and his colleagues have found that even high school physics teachers and experienced bicyclists are subject to the same perceptual error: they think that the reflector’s path loops back on itself.
These comments are pertinent because we do not fully understand how people judge the speed, direction, and position of moving objects. It seems intuitively obvious that to determine the speed of a moving object, you would note its position at time 1, its position at time 2, and the amount of time that elapses between the two. However, this is probably not the way we normally do it. Unrelated factors such as contrast within a pattern or certain spatial features can affect our perception of speed.
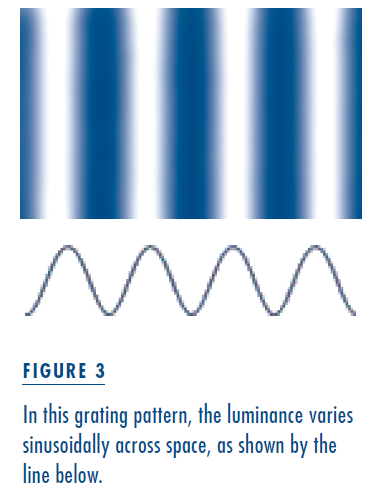Consider a simple striped pattern like that illustrated in Figure 3. If we were to see that pattern through a window and set it in motion (left to right, say), it would appear to move smoothly, and its apparent speed would be closely related to its actual speed. However, if we either reduce the contrast within the pattern (as in Figure 4A) or make the stripes narrower (as in Figure 4B), the apparent speed would decrease even though the actual physical speed doesn’t change. In fact, if we change the stripes from black and white to a carefully balanced red and green, the motion of the pattern might appear to stop entirely even though it continues to move with the same speed. We do not fully understand why we experience such strange and anomalous percepts. In all these cases, we are quite capable of seeing the individual stripes and telling their 
positions, so it’s unlikely that we use this information to judge speed.
The problem of judging the speed of a bicycle from the perceived motion of reflectors on its wheels is complex. In essence, we need to extract the lateral translation and ignore the rotational component of the reflector’s motion. Since our understanding of how the brain interprets speed is incomplete, we’d been unable to predict how well observers would perform if we asked them to judge the speed of an object moving along a cycloidal trajectory.
We devised a simple task that could be carried out using a computer display, rather than going immediately to field tests. We put observers in
a darkened room and asked them to look at a computer monitor. Two white circles appeared against a dark background, one on each side of the screen, one on the upper half and one on the lower half. The two circles began to move towards the midline of the monitor. One moved at a constant speed along a straight path; the other moved along a cycloid path or some variation. We asked the observers to tell us which appeared to be moving faster across the screen. By randomly varying the starting points and the total distance each dot traveled, we ensured that extraneous cues such as time to cross the midline or time of disappearance could not be used.
The results were startling. Virtually every observer thought that the circle moving along a cycloid path was crossing the screen faster than the one moving along a straight path when their actual forward-moving speeds were the same. The error in speed judgment was sometimes quite substantial, as great as 25 percent overestimation for some observers. The consequences of such a large error in estimation can be quite serious. If a driver believes that a bicycle is moving much faster than it really is, for example, he may judge that it will clear an intersection before the car reaches it and accordingly fail to brake at the appropriate time.
Fixing the Problem
We were quite surprised by this result and wondered whether there might be a simple way to reduce or eliminate the perceptual error. Since the illusion seems to be a consequence of the trajectory of the reflector, we thought that the addition of a second reflector at the center of rotation—as though on the axle of a bicycle wheel—might help. We considered removing the reflector from the spoke, but there are compelling arguments against doing so.
A reflector on the axle moves in a straight line at the same speed as the bicycle itself, unlike a reflector on a wheel spoke. However, a single bright dot moving along a straight line does not draw one’s attention as readily as a fluctuating one; nor does it give very useful information about the identity of the object. So we measured the apparent speed of a two-dot configuration, placed as though one were on a spoke and one on
the axle. We thought that the “bouncing” dot would draw attention and help identify the object, while the center dot would give correct information about trajectory and speed. We were startled to find, however, that observers still made errors in estimating speed— but the errors were in the opposite direction. Our subjects now significantly underestimated the forward speed of the moving dots.
This result led us to examine several two- and three-dot configurations that might be fitted to bicycles, hoping to find one or more that would not produce such perceptual errors. We found that when two dots (or reflectors) were placed exactly opposite one another, observers judged the speed without bias or significant error. Three dots evenly spaced around the axle also produced accurate estimates. In general, however, any configuration that included a significant asymmetry in the placement of dots led to perceptual error. Configurations with a dot at the center of rotation produced an underestimation of speed, and those that included an asymmetric arrangement of dots on the spokes or rim led to overestimation.
The apparent slowing in the former case may be related to the characteristics of neurons in cortical area MT, a region of the brain believed to be integrally involved in the analysis of visual motion. Many MT cells respond selectively to objects moving in a particular direction, but their responses are reduced when other objects move in the same direction nearby. These neurons would produce a smaller response to a dot moving at the center of rotation when one or more other dots move nearby as though on the spokes of a wheel.
The perceived increase in speed of a single cycloid or an asymmetric arrangement of dots on a cycloid path suggests a different kind of explanation. The observer’s task is to distinguish the linear speed even though no single visible feature is moving at that speed. Since each of the individual features (dots) is moving along a longer trajectory, the average speed of each must be greater than the linear speed the observer is trying to estimate. Perhaps the observer’s judgment is influenced by the higher average speed of the visible features.
Although these are plausible explanations of the errors in estimating speed, they do not explain the lack of perceptual bias when two (or three) symmetrically placed reflectors are used. In practical terms, of course, it is critical only that we identify which configurations work. Nonetheless, we hope to learn why these particular patterns sidestep perceptual biases.
Our current hypotheses relate to observers’ clear sense of the rotational component of each dot’s motion in several of the configurations we studied. Only when the dots are symmetrically placed does the observer perceive equal forward and backward rotational motion at every moment. There is, of course, no actual backward motion, but the perception is powerful. We wonder whether, in a symmetrical arrangement, the extra speed attributed to the rotation is effectively canceled out, leaving nothing but forward movement to shape observers’ judgments. We hope to come to a more complete understanding with additional research.
There is a further question of interest and relevance. Recall that we always asked the observers to compare the apparent speeds of two targets, one of them moving in a straight line. When the observer matches the two accurately, there is no selective perceptual bias. However, an accurate match on this task does not imply that the apparent speed is identical to the real speed; it merely shows that any error in judging the speed of a single moving dot is repeated in the judgment of the test pattern. We wondered whether our subjects were actually making accurate speed judgments, or whether they were simply consistent in their errors. To find out, we devised a new psychophysical task that does not involve a speed comparison.
We divided a video monitor screen into halves. On one side was an unpatterned gray field. On the other we drew a pattern of random black and white rectangles, with the same average luminance as the gray field (Figure 5). Near the far edge of this random element (RE) field, we drew a black line extending from top to bottom. We told the observer that the black line was a target and that, when the target was hit, it would immediately flash brightly. As the observer watched, a fuzzy white ball appeared at some randomly determined point in the gray field and began to move at a constant speed toward the RE field. When it reached the edge of the RE field, the ball appeared to move behind it, as though it disappeared behind a wall. The observer was told that the ball continued to move towards the target, but it could either speed up or slow down when it moved behind the wall. Once it reached the target line, the line would flash. The observer’s task was to judge whether the ball moved faster when it was visible against the gray field or when it was not visible behind the RE field. By keeping the width of the RE field constant and varying the speed at which the ball moved when it was visible, we could determine what the observer estimated the actual speed to be.
The results were quite surprising. The relationship between real speed and apparent speed on this task was highly inaccurate and disproportionate. We found that at slow speeds, observers consistently overestimated the speed of the moving spot, but at high speeds, they 
consistently (and in some cases dramatically) underestimated its speed. In fact, above a certain intermediate point, increasing the actual speed had little effect on the judged speed over the range we used, and only for a very small set of actual speeds were estimations approximately accurate. Even when we made all the moving spots equal in effective contrast—something that does not generally occur in nature—our observers still made significant errors in judging the speeds, particularly when they were rapid.
We have found only one set of conditions under which our observers consistently judge the speed of a moving spot accurately. When we increase the contrast between the spot and its background, thus increasing the visibility of the spot, judgments are better. Only if we make the contrast as high as possible with our display can observers determine the speed of the moving spot accurately at all speeds.
What to Do
Our studies of apparent speed are not complete, but they suggest two measures that might increase auto drivers’ ability to judge a bicycle’s motion more accurately at night. The first is simple—use two reflectors, not one, on each side of the wheel and place them directly opposite each other. This could be easily and inexpensively accomplished. It would not reduce either the visibility of the bicycle or its ability to attract attention and be properly identified.
The second measure is to increase the effective contrast, and therefore the visibility, of the reflectors. This is a more complex task. Actual contrast depends on two factors: the brightness of the background behind the bicycle, and the amount of light reaching the driver’s eye from the reflector. 
Backgrounds cannot be controlled, and reflectors can return only a portion of the light shining on them. The amount of light reaching them largely depends on the characteristics of the car’s headlights and its position relative to that of the bicycle. These are not readily predictable or controllable. Furthermore, since it must be visible over a wide angle, the reflected light must be dispersed and will thus be less intense in any given direction than the light that reaches the reflector.
Our data suggest that any increase in contrast will increase the accuracy of the driver’s judgment, so it might be worthwhile to replace reflectors with small, bright light sources. Whether this could be done efficiently and without adding significant weight is a question for lighting engineers. Our studies suggest, however, that the potential payoff could be substantial. Not only would bicycles be more visible, but more importantly, drivers would be able to judge their speed more accurately. We might thus increase the safety of bike riders who need to cycle at night.
Further Reading
Edward H. Adelson and J. Anthony Movshon, “Phenomenal Coherence of Moving Visual Patterns,” Nature, vol. 300, pp. 523–525, December 1982.
Dennis R. Proffitt and James E. Cutting, “An Invariant for Wheel-Generated Motions and the Logic of its Determination,” Perception, vol. 9, pp. 435–449, 1980.
Dennis R. Proffitt, James E. Cutting, and David M. Stier, “Perception of Wheel-Generated Motions,” Journal of Experimental Psychology: Human Perception & Performance, vol. 5, pp. 289–302, May 1979.
