The Value of Value Pricing

[sharelines]Road prices can be set to achieve different goals.

Seeking ways to ease highway financing and alleviate traffic congestion, policy makers have put toll roads on the national agenda. The public is skeptical of the idea, to say the least. So the federal government has been sponsoring demonstration projects, both to gain practical experience and to increase public familiarity with road-pricing concepts and the ways they work.

Although most of the demonstrations are merely studies, two are currently operating on real roads in California. They show that the hardware and software work well, that transactions and enforcement are manageable, and that drivers easily adjust to pricing.

One project, the SR91 express lanes in Orange County, is a privately financed ten-mile roadway that parallels the Riverside Freeway (SR91), a notorious bottleneck. Drivers using the new roadway pay electronically according to a fee schedule that varies by time of day and day of week. Three-person carpools use the lanes at a discount. When the new lanes opened, typical peak-hour delays on the original lanes on this ten-mile section fell from over thirty minutes to less than ten minutes.

The second demonstration project, located on an eight-mile section of Interstate 15 (I-15) just north of San Diego, applies a more radical pricing concept. The carpool lanes there were underused, leaving a lot of concrete unoccupied. Solo drivers can now buy their way into this spare capacity, at a price that might change at any moment and that is set to maintain free-flow speeds in the fast lanes. This so-called “dynamic pricing” means that users do not know the exact price until just before they make the lane choice.

Each of these projects is attractive because of the way they use pricing. The SR91 express lanes show that the private sector can finance a needed road by charging tolls. It’s too early to know how successful it will prove to be for its investors, but it has produced none of the close brushes with default that have plagued some other toll roads. The original lanes are still free of charge and are much less congested than before; meanwhile, many people voluntarily pay up to $4.25 for better service on the express lanes. On I-15, similarly, there seem to be no losers: more people have the express-lane option, it is voluntary, and it removes some traffic from the free lanes.

The SR91 express lanes show that the private sector can finance a needed road by charging tolls.

These indications of success are interesting, but they say more about how capacity can be provided than about the nature of road pricing . To evaluate the projects as pricing demonstrations, we need to ask somewhat different questions, such as: what are the advantages and disadvantages of using time-varying prices on roads?

Value Pricing

To answer, we need to look closely at one key feature of both projects: that is, there is a free alternative to the tolled lanes. Free alternatives are not a necessary part of road pricing, but they characterize most of the current examples of it. The term “value pricing” is being applied to situations offering a choice like this, the idea being that one has the opportunity to pay to get extra value. The term, coined to market the SR91 express lanes, proved so attractive that Congress applied it to the entire demonstration program when it was reauthorized in 1998 (although its previous name, “congestion pricing,” more accurately describes the projects).

As a demonstration of pricing, however, the concept has an Achilles’ heel. To show the difference that pricing can make, it is essential that there be significant speed differences between free and priced roadways. This means that the free roadway must remain congested; if improvements on it or on parallel routes were to eliminate heavy traffic, there would no longer be an incentive to pay a toll. Such projects can work only if we fail to make significant progress toward reducing congestion overall. Herein lies a political volcano waiting to explode.

Vulnerability exists whether the project is private or public. Suppose you are an entrepreneur thinking of building a toll road parallel to an existing congested road. You need to recoup your investment from the toll revenue, so you include a “non-compete” clause in your contract that says the state highway agency must promise not to build new capacity that would reduce congestion on the existing road. This is exactly the situation on SR91, where the operator recently invoked this franchise provision and ignited a great controversy. (Resentment was exacerbated by the operator’s attempt to sell out to a newly created nonprofit corporation.) Or suppose you are a public agency opening an existing carpool lane to paying solo drivers. To maintain the service for carpools, you cannot let too many cars onto the express lanes; and in order to have anything to exchange for the prices you charge, solo drivers must save a substantial amount of time.

So, whether the express roadway is public or private, the need to recoup costs or retain incentives for carpoolers requires tolls high enough to restrict use of the faster roadway significantly. By contrast, if the objective were to reduce total travel delay for all travelers, the operator would set low tolls, attract more users to the faster roadway, and thereby also speed up the slower roadway.

How Much Difference Does It Make?

These problems are quantified in two studies in which I’ve participated—the first with Jia Yan, the second with Erik Verhoef. Happily, the studies also identify a number of factors that alleviate these problems. We use simulations because we want to explore pricing options that could have been adopted but weren’t—including not pricing anything, which we take as the default option. To focus on pricing, we compare current policies with other possible uses of the total capacity that now exists, not with the situation before the new lanes were built.

It turns out that one critical factor is user diversity. After all, an underlying rationale for value pricing is the idea that choice is beneficial because people are not all alike. So we describe different types of motorists by assigning them different time values, i.e., different trade-offs between time and money savings. The study with Yan does this by defining two types of solo drivers, one with a high and one with a low time value; in addition, it assumes there are three-person carpools with time value per person equal to the solo drivers’ average. The study with Verhoef uses a continuum of time values, based on surveys in the Netherlands.

Another critical factor is the size of the toll. Rather than arbitrarily setting prices, we define several alternative objectives and compute a toll to meet each objective. We then estimate the resulting traffic speeds and densities. Finally, we compute the net benefits of the policy, relative to a policy of no toll.Net benefits relate to all users, being the total value of their trips minus the total time costs. Toll payments are not subtracted, nor are toll revenues added—that is, we assume that benefits lost to users through toll payments are balanced by benefits gained in the public sector from using toll revenues.

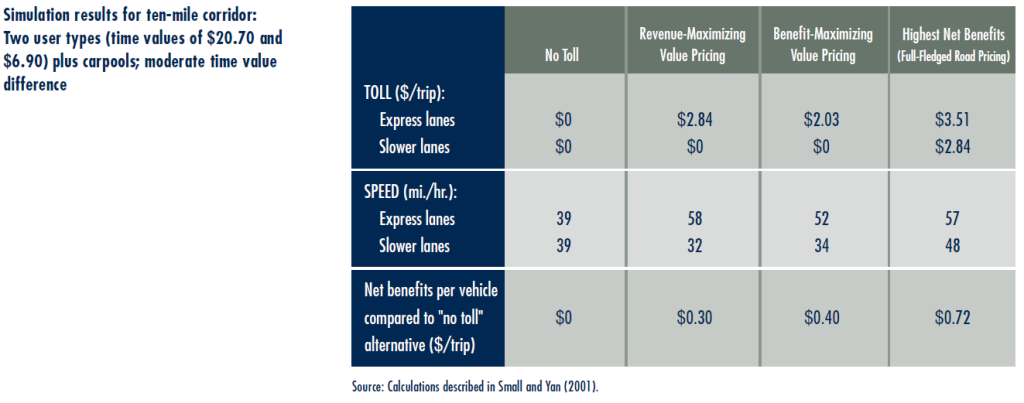
Results for State Route 91

We calibrated parameters for the simulations to match conditions on SR91 in summer 1997. The table shows results for a case where the time values of solo drivers are $20.70 and $6.90 per hour. We assume carpools of three or more people use the express lanes for free, as was the practice on SR91 in summer 1997. We define three types of pricing strategies:

Revenue –Maximizing Value Pricing: The express toll is set to maximize revenues, given that the rest of the road is free.
Benefit-Maximizing Value Pricing: The express toll is set to maximize net benefits, given that the rest of the road is free.
Highest Net Benefits: Tolls are charged on both roadways, and set to maximize net benefits.

The first column of numbers in the table shows the effects of a zero toll on both roadways. Traffic equalizes at a speed of 39 mph. Net benefit is $0, since this is the baseline against which we compute benefits of other policies. It’s not a representation of any actual situation, because we assume new capacity exists but is unpriced.

The second column portrays the situation in summer 1997, in which the operator maximizes revenue. The toll we calculate is $2.84, very close to the toll of $2.75 actually charged at that time (parameters of the model were in fact calibrated to achieve this match). Speeds are 58 mph on the express roadway, but only 32 mph on the regular roadway. Net benefits average $0.30 per vehicle. These benefits arise from two sources: high- time-value cars (including carpools) are sped up at the expense of low-time-value cars, and some less important trips are removed entirely from the peak period.

The third column shows another form of value pricing, which maximizes net benefits when most of the road must remain unpriced. The toll is lower—$2.03—and net benefits compared to the no-toll case are higher, averaging $0.40 per vehicle.

The last column shows how dramatically full-fledged road pricing would differ from even the best case of value pricing. Here, both roadways are priced, with prices set to maximize net benefits. Because users are diverse, this best-case policy still offers two options: $3.51 for a fast trip and $2.84 for a slightly slower trip. In equilibrium, carpools and high-time-value solo drivers choose the faster road. Net benefits are almost twice that of other scenarios, averaging $0.72 per vehicle.

The table shows that the revenue-maximizing toll is 40 percent higher than the benefit-maximizing value-priced toll, and its net benefits are 25 percent less. The higher toll creates too much of a quality differential between the two roadways. The same is true of another scenario, analyzed but not shown here, which replicates the legal restrictions imposed on I-15 in San Diego: traffic on the express lanes must be kept low enough to provide Level of Service C.

The higher toll creates too much of a quality differential between the two roadways.

The table also shows that the benefits of value pricing are not very large—only forty cents per trip or less. The reason is that this ten-mile segment was not very congested in summer 1997, when average peak-period travel delay on the free lanes was only eight minutes. However, by 1998 this delay had already grown to thirteen minutes. In simulations where we consider projected traffic growth, we find much bigger effects from pricing.

Finally, the table shows that neither of the value-pricing scenarios comes close to achieving the full potential benefits of road pricing. It may be worth sacrificing these benefits for the political appeal of offering people a choice to pay or not, but this poses a risk: the whole concept of pricing may be endangered because one imperfect form of it does not provide sufficient benefits.

Our simulations can answer other interesting questions. For example, who stands to lose when we adopt value pricing on a previously free road? Allowing for many types of users, Verhoef and I obtain a surprising answer: it’s not the people with lowest time value, but rather those with intermediate values, who suffer most or gain least. This is because offering only two choices allows the policy to cater only to people at the high and low ends of the distribution. It’s as though the only options in air travel were propeller planes or supersonic jets; a lot of people would be left wishing for something in between.

Factors Favoring Value Pricing

By varying key parameters in our simulations, we can identify a number of factors that improve the performance of value pricing:

Greater diversity of users. The more users’ time values differ from each other, the more benefits the value-pricing scenarios At the other end of the scale, where users are all alike, revenue-maximizing value pricing confers negative benefits—that is, it is worse than not pricing at all.
Higher demand elasticity. The results described above assume that few people will stop using the corridor if conditions worsen or the price If instead demand is very sensitive, and people readily change their routes or modes, the revenue-maximizing toll performs better because it significantly curtails total peak-period traffic, increasing net benefits.
Inherent route differences. Suppose the toll road is faster not just because of less congestion, but because it is shorter or better Verhoef and I find that the benefits from value pricing are then greater.

Another factor improves the performance of some but not all types of value pricing:

Pricing more of the capacity. Typically, less than half the capacity is priced. What if instead most of the capacity were priced? Both studies find that this would dramatically increase the effectiveness of benefit-maximizing value pricing. However, revenue-maximizing pricing performs poorly under this scenario.

Conclusion

Value pricing is hard to do right. It works only when the unpriced part of the network remains congested, and it works best when the price charged and quality offered are both on the low side. But these are pitfalls if you want to use value pricing to demonstrate principles of road pricing. If the configuration is not quite right for success, there is a good chance that the concept of road pricing in general will be tarnished in the minds of policy makers and the public.

Furthermore, the benefits of value pricing depend strongly on the diversity of users. This makes it all the more important to increase our knowledge of people’s varying attitudes about time and money savings. It also highlights an interesting potential role for private enterprise, which has proven adept at identifying and exploiting user diversity in several deregulated transportation industries.

Road pricing seems neither the wave of the future, nor an idea whose time is gone, and we are likely to see more experimentation. This creates opportunities for researchers to help guide experiments in promising directions.